基础算法0x00 回溯_Dfs
开个新坑,记录一下基础算法的学习,顺便准备一下明年的蓝桥杯,整整300大米呢:smile:
参考灵神的视频以及自己做的题,把最近一周写的dfs题分为三类,一类是子集型回溯,一类是组合型回溯,一类是矩阵上的回溯
回溯三问
- 边界条件是什么?
- 子问题是什么?
- 当前操作要做什么?
想对这三个问题,回溯类的题目就很好解决了。
也可以通过画树状图的方式来思考回溯问题
子集型回溯
题目
Leetcode 78 子集Ⅰ
78. 子集Ⅰ
可以从两种角度看这道题
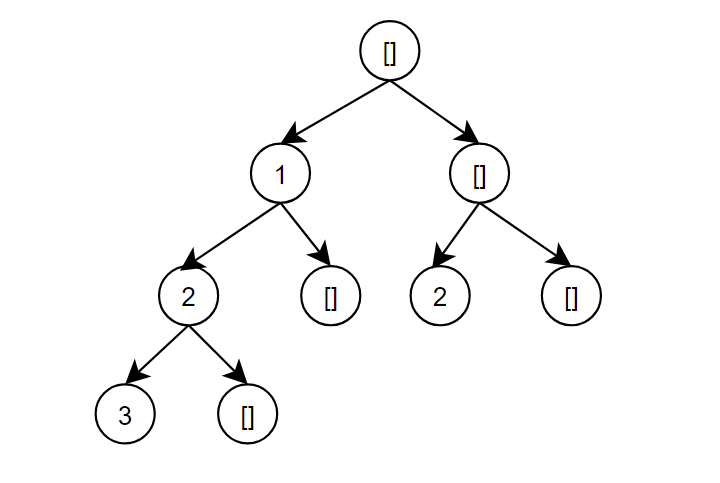
一、选或不选
从选或者不选角度来看
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
vector<vector<int>> ans;
vector<int> path;
void dfs(int i, vector<int>& nums){
int n = nums.size();
if (i == n){
return;
}
dfs(i+1, nums);
path.emplace_back(nums[i]);
dfs(i+1, nums);
path.pop_back();
}
|
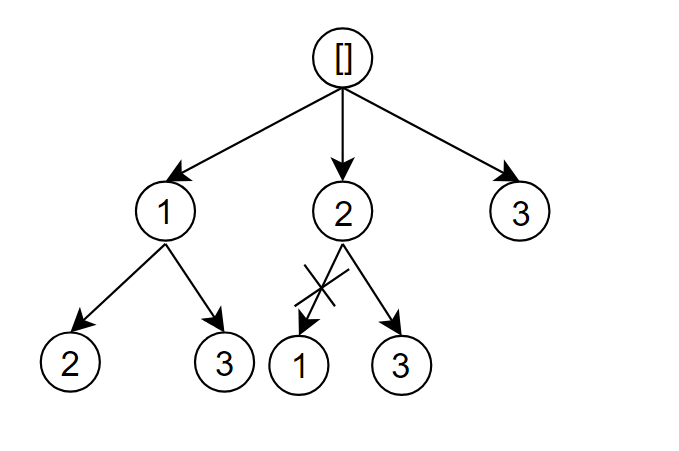
二、选哪个数
从选择哪个数的角度来看
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| vector<vector<int>> ans;
vector<int> path;
void dfs(int i, vector<int>& nums){
int n = nums.size();
if (i == n){
return;
}
for (int j = i; j < n; j++){
path.emplace_back(nums[j]);
ans.emplace_back(path);
dfs(j + 1, nums);
path.pop_back();
}
}
|
主函数中需要先处理好空集
Leetcode 90 子集Ⅱ
90. 子集 II
和第一题的区别在于引入了重复元素,会导致答案出现重复,因此需要引入剪枝操作,剔除重复元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| void dfs(int i, vector<int>& nums){
int n = nums.size();
if (i == n){
return;
}
for (int j = i; j < n; j++){
if (j > i && nums[j] == nums[j - 1])
continue;
path.emplace_back(nums[j]);
ans.emplace_back(path);
dfs(j + 1, nums);
path.pop_back();
}
}
|
组合型回溯
题目
Leetcode 39 组合总数
39. 组合总和
首先对数组进行排序,在遍历过程中加上一个判断即可进行剪枝,如果当前元素加入组合后无法满足条件,那么后面的元素更无法满足,可以break返回。
边界条件:当路径内所有数字求和后等于target即到达边界
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| vector<vector<int>> ans;
vector<int> path;
void dfs(vector<int>& candidates, int target, int i){
if (target == 0){
ans.emplace_back(path);
return;
}
for (int j = i; j < candidates.size(); j++){
if (target - candidates[i] < 0){
break;
}
path.emplace_back(candidates[j]);
dfs(candidates, target - candidates[j], j);
path.pop_back();
}
}
|
矩阵上的dfs
题目
Leetcode 200 岛屿数量
200. 岛屿数量
经典的图论dfs,遍历矩阵中的每一个点,如果是陆地就ans++,同时以这个点为起点进行深度优先搜索,将所有经过的点标记为’0’,避免重复计数,最后按照上右下左的顺序进入下一层。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
int m = grid.size(), n = grid[0].size(), ans = 0;
function<void(int, int)> dfs = [&](int i, int j){
if (i < 0 || i > m - 1 || j < 0 || j > n - 1 || grid[i][j] == '0'){
return;
}
grid[i][j] = '0';
dfs(i-1,j);
dfs(i,j+1);
dfs(i+1,j);
dfs(i,j-1);
};
for (int i = 0; i < m; i++){
for (int j = 0; j < n; j++){
if (grid[i][j] == '1'){
ans++;
dfs(i, j);
}
}
}
return ans;
}
};
|
Leetcode 79 单词搜索
79. 单词搜索
同样也是在矩阵上搜索,相比上一道海岛统计,这道题需要使用状态恢复,因为从下一个点开始的搜索依然要搜索这些点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public:
bool exist(vector<vector<char>>& board, string word) {
int m = board.size(), n = board[0].size();
function<bool(int, int, int)> dfs = [&](int i, int j, int k){
if (k == word.length()){
return true;
}
if (i < 0 || j < 0 || i > m - 1 || j > n - 1 || board[i][j] != word[k]){
return false;
}
board[i][j] = '\0';
bool res = dfs(i-1,j,k+1) || dfs(i,j+1,k+1) || dfs(i+1,j,k+1) || dfs(i,j-1,k+1);
board[i][j] = word[k];
return res;
};
for (int i = 0; i < m; i++){
for (int j = 0; j < n; j++){
if (dfs(i, j, 0))
return true;
}
}
return false;
}
};
|
Leetcode 51 N皇后
51. N 皇后
烧鸡100题里面唯一一道回溯困难,一年前很难写出完整的代码,现在轻松拿下。
把每一行都单独拿出来,在这一行中遍历每一列寻找可以防止皇后的点位,这就是子问题,引入valid(i, j)函数判断是否可以合法放置皇后。
valid(i, j)函数遍历之前的i - 1行,检查是否会被之前放置的皇后攻击。最后记得状态恢复。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public:
vector<vector<string>> solveNQueens(int n) {
vector<string> chess(n, string(n,'.'));
vector<vector<string>> ans;
function<bool(int, int)> valid = [&](int i, int j){
for (int k = 0; k < i; k++){
if (chess[k][j] == 'Q' || (k-i+j >= 0 && k-i+j < n && chess[k][k-i+j] == 'Q') || (i+j-k >= 0 && i+j-k < n && chess[k][i+j-k] == 'Q')) return false;
}
return true;
};
function<void(int)> dfs = [&](int i){
if (i == n){
ans.emplace_back(chess);
return;
}
for (int j = 0; j < n; j++){
if (valid(i, j)){
chess[i][j] = 'Q';
dfs(i+1);
chess[i][j] = '.';
}
}
};
dfs(0);
return ans;
}
};
|

